Golden Ratio
In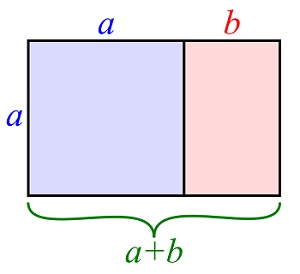 mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure on the right illustrates the geometric relationship. Expressed algebraically, for quantities a and b with a > b > 0,
mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure on the right illustrates the geometric relationship. Expressed algebraically, for quantities a and b with a > b > 0,
where the Greek letter phi (φ or Φ) represents the golden ratio. Its value is:
The golden ratio is also called the golden mean or golden section. Other names include extreme and mean ratio, medial section, divine proportion, divine section, golden proportion, golden cut, and golden number.
Some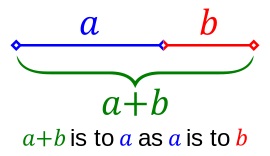 twentieth-century artists and architects, including Le Corbusier and Dalí, have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing. The golden ratio appears in some patterns in nature, including the spiral arrangement of leaves and other plant parts.
twentieth-century artists and architects, including Le Corbusier and Dalí, have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing. The golden ratio appears in some patterns in nature, including the spiral arrangement of leaves and other plant parts.
Mathematicians since Euclid have studied the properties of the golden ratio, including its appearance in the dimensions of a regular pentagon and in a golden rectangle, which may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has also been used to analyze the proportions of natural objects as well as man-made systems such as financial markets, in some cases based on dubious fits to data.
History
The golden ratio has been claimed to have held a special fascination for at least 2,400 years, although without reliable evidence. According to Mario Livio:
Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. But the fascination with the Golden Ratio is not confined just to mathematicians. Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.
Ancient Greek mathematicians first studied what we now call the golden ratio because of its frequent appearance in geometry. The division of a line into "extreme and mean ratio" (the golden section) is important in the geometry of regular pentagrams and pentagons. Euclid's Elements provides the first known written definition of what is now called the golden ratio:
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.
Euclid explains a construction for cutting (sectioning) a line "in extreme and mean ratio" (i.e., the golden ratio). Throughout the Elements, several propositions (theorems in modern terminology) and their proofs employ the golden ratio.
The golden ratio is explored in Luca Pacioli's book De divina proportione (1509).
The first known approximation of the (inverse) golden ratio by a decimal fraction, stated as "about 0.6180340", was written in 1597 by Michael Maestlin of the University of Tübingen in a letter to his former student Johannes Kepler.
Since the 20th century, the golden ratio has been represented by the Greek letter φ (phi, after Phidias, a sculptor who is said to have employed it) or less commonly by τ (tau, the first letter of the ancient Greek root τομή—meaning cut).
Applications and Observations
Aesthetics
De Divina Proportione, a three-volume work by Luca Pacioli, was published in 1509. Pacioli, a Franciscan friar, was known mostly as a mathematician, but he was also trained and keenly interested in art. De Divina Proportione explored the mathematics of the golden ratio. Though it is often said that Pacioli advocated the golden ratio's application to yield pleasing, harmonious proportions, Livio points out that the interpretation has been traced to an error in 1799, and that Pacioli actually advocated the Vitruvian system of rational proportions. Pacioli also saw Catholic religious significance in the ratio, which led to his work's title. De Divina Proportione contains illustrations of regular solids by Leonardo da Vinci, Pacioli's longtime friend and collaborator; these are not directly linked to the golden ratio.
Architecture The Parthenon's façade as well as elements of its façade and elsewhere are said by some to be circumscribed by golden rectangles. Other scholars deny that the Greeks had any aesthetic association with golden ratio. For example, Midhat J. Gazalé says, "It was not until Euclid, however, that the golden ratio's mathematical properties were studied. In the Elements (308 BC) the Greek mathematician merely regarded that number as an interesting irrational number, in connection with the middle and extreme ratios. Its occurrence in regular pentagons and decagons was duly observed, as well as in the dodecahedron (a regular polyhedron whose twelve faces are regular pentagons). It is indeed exemplary that the great Euclid, contrary to generations of mystics who followed, would soberly treat that number for what it is, without attaching to it other than its factual properties." And Keith Devlin says, "Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. In fact, the entire story about the Greeks and golden ratio seems to be without foundation. The one thing we know for sure is that Euclid, in his famous textbook Elements, written around 300 BC, showed how to calculate its value." Later sources like Vitruvius exclusively discuss proportions that can be expressed in whole numbers, i.e. commensurate as opposed to irrational proportions.
The Parthenon's façade as well as elements of its façade and elsewhere are said by some to be circumscribed by golden rectangles. Other scholars deny that the Greeks had any aesthetic association with golden ratio. For example, Midhat J. Gazalé says, "It was not until Euclid, however, that the golden ratio's mathematical properties were studied. In the Elements (308 BC) the Greek mathematician merely regarded that number as an interesting irrational number, in connection with the middle and extreme ratios. Its occurrence in regular pentagons and decagons was duly observed, as well as in the dodecahedron (a regular polyhedron whose twelve faces are regular pentagons). It is indeed exemplary that the great Euclid, contrary to generations of mystics who followed, would soberly treat that number for what it is, without attaching to it other than its factual properties." And Keith Devlin says, "Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. In fact, the entire story about the Greeks and golden ratio seems to be without foundation. The one thing we know for sure is that Euclid, in his famous textbook Elements, written around 300 BC, showed how to calculate its value." Later sources like Vitruvius exclusively discuss proportions that can be expressed in whole numbers, i.e. commensurate as opposed to irrational proportions.
The Swiss architect Le Corbusier, famous for his contributions to the modern international style, centered his design philosophy on systems of harmony and proportion. Le Corbusier's faith in the mathematical order of the universe was closely bound to the golden ratio and the Fibonacci series, which he described as "rhythms apparent to the eye and clear in their relations with one another. And these rhythms are at the very root of human activities. They resound in man by an organic inevitability, the same fine inevitability which causes the tracing out of the Golden Section by children, old men, savages and the learned."
Le Corbusier explicitly used the golden ratio in his Modulor system for the scale of architectural proportion. He saw this system as a continuation of the long tradition of Vitruvius, Leonardo da Vinci's "Vitruvian Man", the work of Leon Battista Alberti, and others who used the proportions of the human body to improve the appearance and function of architecture. In addition to the golden ratio, Le Corbusier based the system on human measurements, Fibonacci numbers, and the double unit. He took suggestion of the golden ratio in human proportions to an extreme: he sectioned his model human body's height at the navel with the two sections in golden ratio, then subdivided those sections in golden ratio at the knees and throat; he used these golden ratio proportions in the Modulor system. Le Corbusier's 1927 Villa Stein in Garches exemplified the Modulor system's application. The villa's rectangular ground plan, elevation, and inner structure closely approximate golden rectangles.
Painting
Leonardo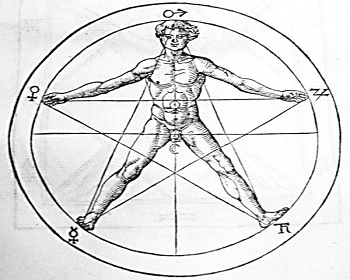 da Vinci's illustrations of polyhedra in De divina proportione (On the Divine Proportion) and his views that some bodily proportions exhibit the golden ratio have led some scholars to speculate that he incorporated the golden ratio in his paintings. But the suggestion that his Mona Lisa, for example, employs golden ratio proportions, is not supported by anything in Leonardo's own writings. Similarly, although the Vitruvian Man is often shown in connection with the golden ratio, the proportions of the figure do not actually match it, and the text only mentions whole number ratios.
da Vinci's illustrations of polyhedra in De divina proportione (On the Divine Proportion) and his views that some bodily proportions exhibit the golden ratio have led some scholars to speculate that he incorporated the golden ratio in his paintings. But the suggestion that his Mona Lisa, for example, employs golden ratio proportions, is not supported by anything in Leonardo's own writings. Similarly, although the Vitruvian Man is often shown in connection with the golden ratio, the proportions of the figure do not actually match it, and the text only mentions whole number ratios.
Salvador Dalí, influenced by the works of Matila Ghyka, explicitly used the golden ratio in his masterpiece, The Sacrament of the Last Supper. The dimensions of the canvas are a golden rectangle. A huge dodecahedron, in perspective so that edges appear in golden ratio to one another, is suspended above and behind Jesus and dominates the composition.
Music
Ernő Lendvai analyzes Béla Bartók's works as being based on two opposing systems, that of the golden ratio and the acoustic scale, though other music scholars reject that analysis. French composer Erik Satie used the golden ratio in several of his pieces, including Sonneries de la Rose+Croix. The golden ratio is also apparent in the organization of the sections in the music of Debussy's Reflets dans l'eau (Reflections in Water), from Images (1st series, 1905), in which "the sequence of keys is marked out by the intervals 34, 21, 13 and 8, and the main climax sits at the phi position."
The musicologist Roy Howat has observed that the formal boundaries of La Mer correspond exactly to the golden section. Trezise finds the intrinsic evidence "remarkable," but cautions that no written or reported evidence suggests that Debussy consciously sought such proportions.
Nature Adolf Zeising, whose main interests were mathematics and philosophy, found the golden ratio expressed in the arrangement of parts such as leaves and branches along the stems of plants and of veins in leaves. He extended his research to the skeletons of animals and the branchings of their veins and nerves, to the proportions of chemical compounds and the geometry of crystals, even to the use of proportion in artistic endeavors. In these patterns in nature he saw the golden ratio operating as a universal law. In connection with his scheme for golden-ratio-based human body proportions, Zeising wrote in 1854 of a universal law "in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form."
Adolf Zeising, whose main interests were mathematics and philosophy, found the golden ratio expressed in the arrangement of parts such as leaves and branches along the stems of plants and of veins in leaves. He extended his research to the skeletons of animals and the branchings of their veins and nerves, to the proportions of chemical compounds and the geometry of crystals, even to the use of proportion in artistic endeavors. In these patterns in nature he saw the golden ratio operating as a universal law. In connection with his scheme for golden-ratio-based human body proportions, Zeising wrote in 1854 of a universal law "in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form."
In 2010, the journal Science reported that the golden ratio is present at the atomic scale in the magnetic resonance of spins in cobalt niobate crystals.
Since 1991, several researchers have proposed connections between the golden ratio and human genome DNA.
However, some have argued that many apparent manifestations of the golden ratio in nature, especially in regard to animal dimensions, are fictitious.
Perceptual Studies
Studies by psychologists, starting with Fechner, have been devised to test the idea that the golden ratio plays a role in human perception of beauty. While Fechner found a preference for rectangle ratios centered on the golden ratio, later attempts to carefully test such a hypothesis have been, at best, inconclusive.
Disputed Observations
Examples of disputed observations of the golden ratio include the following:
- Historian John Man states that the pages of the Gutenberg Bible were "based on the golden section shape". However, according to Man's own measurements, the ratio of height to width was 1.45.
- Some specific proportions in the bodies of many animals (including humans) and parts of the shells of mollusks are often claimed to be in the golden ratio. There is a large variation in the real measures of these elements in specific individuals, however, and the proportion in question is often significantly different from the golden ratio. The ratio of successive phalangeal bones of the digits and the metacarpal bone has been said to approximate the golden ratio. The nautilus shell, the construction of which proceeds in a logarithmic spiral, is often cited, usually with the idea that any logarithmic spiral is related to the golden ratio, but sometimes with the claim that each new chamber is proportioned by the golden ratio relative to the previous one; however, measurements of nautilus shells do not support this claim.
- In investing, some practitioners of technical analysis use the golden ratio to indicate support of a price level, or resistance to price increases, of a stock or commodity; after significant price changes up or down, new support and resistance levels are supposedly found at or near prices related to the starting price via the golden ratio. The use of the golden ratio in investing is also related to more complicated patterns described by Fibonacci numbers (e.g. Elliott wave principle and Fibonacci retracement). However, other market analysts have published analyses suggesting that these percentages and patterns are not supported by the data.
Source: Golden Ratio


